Лаборатория стохастических задач
Заведующая лабораторией д.ф.-м.н. Нина Александровна Каргаполова (nkargapolova@sscc.ru).
В составе лаборатории 6 кандидатов и 6 докторов наук, 1 молодой научный сотрудник.
Сабельфельд К.К., Левыкин Ф.И., Войтишек А.В. Ухинова О.С., Каблукова Е.Г., Каргаполова Н.А., Киреева А.Е., Шалимова И.А.,
Огородников В.А., Каргин Б.А., Акентьева М.С.
Тематика:
– разработка теории и методов стохастического моделирования для решения многомерных краевых задач математической физики в детерминированной и стохастической постановках, направленных на решение прикладных задач: исследование турбулентных течений, формирование кластеров в фазовых переходах и кинетика их роста, дифракция рентгеновского излучения на дислокациях в кристаллах, транспорт экситонов и задачи фотоники;
– разработка и исследование численных методов моделирования случайных процессов и полей с приложениями к задачам вычисления радиационного баланса аэрозольной облачной атмосферы и радиационных потоков в системе "океан – атмосфера" с учетом ветрового волнения поверхности океана;
– построение численных статистических моделей переноса нестационарных лазерных сигналов для решения дистанционного наземного лидарного зондирования аэрозольной атмосферы и облаков различных форм, а также аэрокосмического лазерного зондирования облачности и поверхности океана;
– численное решение задач статистической метеорологии: разработка и реализация эффективных стохастических генераторов погоды, оценка и прогнозирование экстремальных метеорологических явлений, разработка и исследование моделей случайных пространственно-временных полей биоклиматических индексов в различных регионах страны.
История лаборатории
В 1979 году решением Ученого совета Вычислительного центра СО АН СССР на базе группы сотрудников лаборатории методов Монте-Карло, возглавляемой членом-корреспондентом АН СССР Г.А. Михайловым, была создана лаборатория оптики дисперсных сред. В состав лаборатории также вошла группа сотрудников бывшей лаборатории статистической метеорологии, руководителем которой был д.ф.-м.н., профессор А.С. Марченко.
Первоначально основными научными направлениями лаборатории были численное статистическое моделирование задач оптики аэрозольной облачной атмосферы, включая задачи наземного и аэрокосмического лазерного зондирования атмосферы, земной поверхности и океана, а также задачи статистической метеорологии. Руководителем лаборатории был избран к.ф.-м.н. (с 1986 г. – д.ф.-м.н.) Б.А. Каргин. Позже, в связи с кадровыми изменениями, лаборатория оптики дисперсных сред была преобразована в лабораторию стохастических задач с соответствующей корректировкой тематики.
Важнейшие достижения
Компьютерное моделирование транспорта электронов в сильных электрических полях в низкоразмерных гетероструктурах
проф. д.ф.-м.н. Сабельфельд К.К., к.ф.-м.н. Каблукова Е.Г., к.ф.-м.н. Протасов Д.Ю., д.ф.-м.н. Журавлев К.С.
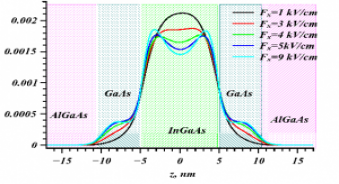
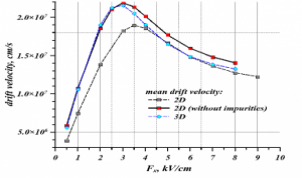
С помощью разработанного в лаборатории стохастических задач программного комплекса для решения системы уравнений Шредингера-Пуассона-Больцмана для задачи переноса заряженных частиц в двумерной полупроводниковой гетероструктуре проведено моделирование движения электронов в легированной примесями (донорами и акцепторами) гетероструктуре AlGaAs/GaAs/InGaAs/GaAs/AlGaAs, оценены зависимости средних дрейфовых скоростей электронов от напряженности внешнего электрического с учетом рассеяния на примесях, полярных оптических и междолинных фононах. В результате моделирования было обнаружено отсутствие пространственного переноса электронов в широкозонные слои AlGaAs из-за высоких барьеров, создаваемых легированными примесями. Расчет показал, что уменьшенное рассеяние горячих электронов в гетероструктуре DA-pHEMT за счет эффектов квантования приводит к увеличению скорости дрейфа в сильных электрических полях, что открывает новые возможности для улучшения гетероструктур и повышения производительности СВЧ-транзисторов. Исследование выполнено в сотрудничестве с группой физиков из Института физики полупроводников им. А.В.Ржанова СО РАН.
Работа выполнена при поддержке гранта РНФ 19-11-00019.
Результаты исследований опубликованы в работах:
1. Kablukova E. G., Sabelfeld K. K., Protasov D., Zhuravlev K. Stochastic simulation of electron transport in a strong electrical field in low-dimensional heterostructures // Monte Carlo Methods Appl, 2023, V. 29, No 4, p. 307–322. DOI: 10.1515/mcma-2023-2019
2. Kuznetsov V. A., Protasov D. Y., Kostyuchenko V. Y., Sabelfeld K. K., Kablukova E. G. Hall Effect in Strong Electric Fields in AlGaAs/InGaAs/GaAs Heterostructures with Donor-Acceptor Doping // International Conference of Young Specialists on Micro/ Nanotechnologies and Electron Devices, EDM, 2023, pp. 90–93. DOI: 10.1109/EDM58354.2023.10225239
Реализован алгоритм решения стационарного уравнения Ламе для двумерной области с помощью рандомизированного векторного алгоритма. Уравнение Ламе записывается как система уравнений анизотропной диффузии для компонент решения по каждому направлению u = (u1, u2). Правая часть уравнений для u1 и u2 содержит смешанные производные от второй компоненты решения, т.е. производную от u2 для уравнения на u1 и производную от u1 для уравнения на u2. Для решения системы уравнений используется итерационный алгоритм, на каждом шаге которого решается уравнение анизотропной диффузии с правой частью, содержащей производную от решения на предыдущей итерации. Конечно-разностная аппроксимация уравнения анизотропной диффузии решается с помощью рандомизированного векторного алгоритма решения систем линейных алгебраических уравнений (СЛАУ) вида x=Ax+b, представленного в [1]. Этот алгоритм основан на рандомизированном вычислении ряда Неймана . Для приведения СЛАУ к нужному виду x=Ax+b и улучшению спектральных свойств матрицы A используется красно-чёрное упорядочивание узлов сетки и преобразование к матричному виду метода Гаусса–Зейделя. Для ускорения расчётов реализована параллельная версия алгоритма путём распределения независимых траекторий, вычисляющих решение СЛАУ, между MPI-процессами. На рис. 1 представлены результаты численного решения уравнения Ламе для двумерной сетки размером 52×52 узла, что соответствует размеру СЛАУ N=2500. Точность решения зависит от количества траекторий Т рандомизированного алгоритма решения СЛАУ. На графиках показаны результаты для Т=106 и Т=107. Видно, что решение уравнения Ламе «u_1e6» совпадает с точным значением u* уже для Т=106. В значениях производной «d_1e6» присутствует шум, который уменьшается при увеличении числа траекторий Т. Например, значения «d_1e7», вычисленные для Т=107, ближе к точным значениям производной d*, чем значения «d_1e6», вычисленные для Т=106. Время решения уравнения Ламе при использовании 48 MPI-процессов кластера “МВС-10П” составляет 30.2 секунды.
Изучались алгоритмы компенсационного суммирования, которые позволяют уменьшить погрешность при сложении большого числа слагаемых. В частности, исследовалась способность алгоритмов компенсационного суммирования уменьшать погрешность при решении задач методом Монте-Карло. Проблема является актуальной, так как в последнее время достаточно широко применяются алгоритмы смешанной точности, когда часть вычислений для увеличения быстродействия проводится с переменными пониженной разрядности. На тестовых вычислениях эмпирических средних случайных величин было показано, что при использовании переменных с одинарной точностью могут возникать большие ошибки. Применение алгоритмов компенсационного суммирования позволяет эти ошибки существенно уменьшить. Были изучены три алгоритма компенсационного суммирования, наилучшим из которых показал себя алгоритм Кэхэна.
Методом Монте-Карло изучались процессы переноса оптического излучения в водном слое и проводились расчёты характеристик глубинного режима светового поля. Вычисления проводились для двух моделей водной среды различной степени прозрачности. Методом Монте-Карло оценивались угловые распределения освещённости на разных глубинах. Для определения оптического глубинного режима предложена методика на основе статистик Колмогорова – Смирнова и Пирсона.
Разработаны три подхода по выбору константы в выражении для погрешности метода Монте-Карло для вычисления математического ожидания случайной величины : по вероятности, в среднеквадратическом и в среднем. В практических исследованиях по методу Монте-Карло при оценке погрешности вычислений рекомендовано использовать подход «в среднем» с константой
Разработаны специальные модели многомерных распределений в виде смесей нормальных распределений и построены алгоритмы моделирования некоторых типов условных процессов. Рассматривается представление многомерной плотности распределения вектора, состоящего из двух подвекторов, в виде произведения двух плотностей. Первая представляет собой взвешенную сумму двух многомерных нормальных плотностей, а вторая – взвешенную сумму двух многомерных условных нормальных плотностей. Число переменных в этих плотностях соответствует размерности подвекторов рассматриваемого вектора. Получено выражение для итоговой плотности, состоящей из взвешенной суммы четырех нормальных распределений, а также исследованы свойства этого распределения. В частности, показано, что для определенного класса ковариационных матриц итоговое распределение вероятностей имеет вид смеси двух нормальных распределений. Для случая, когда параметры компонентов смеси известны, построены алгоритмы моделирования условных и безусловных случайных векторов, учитывающих специфику рассмотренных распределений. Для моделирования стационарных скалярных случайных рядов на основе реальных данных с распределениями в виде смеси двух нормальных распределений с учетом корреляционных связей между смежными элементами ряда разработан алгоритм, включающий в себя известный ЕМ алгоритм для разделения компонентов смеси, последовательное применение метода условных распределений для каждого элемента ряда и метод исключения для построения соответствующих условных реализаций. Векторные стационарные ряды, например, совместные ряды минимальной и максимальной за сутки температуры воздуха с двумерными распределениями в виде смеси двух нормальных распределений, учитывающие межсуточные корреляционные связи строятся аналогично, но соответствующий алгоритм является более трудоемким, главным образом за счет метода исключения.
Проводятся исследования по разработке новых алгоритмов численного статистического моделирования процессов и полей гидрометеорологических параметров с заданными одномерными распределениями и корреляциями на основе данных многолетних наблюдений на отдельных метеорологических станциях, а также на сети метостанций, расположенных в различных климатических зонах Восточной Сибири и Дальнего Востока. При этих исследованиях возникает необходимость решать задачи большой размерности и трудоемкости. В связи с этим, проводятся работы по реализации алгоритмов моделирования негауссовских процессов с использованием технологий параллельного программирования.
Разработан алгоритм метода Монте-Карло для численного моделирования процесса переноса оптического излучения в рассеивающих средах, рассеивающими элементами которых являются прозрачные или полупрозрачные кристаллические частицы. Главное внимание в работе уделено решению одной из важнейших задач атмосферной оптики – исследованию переноса солнечного излучения в перистых облаках, состоящих из ледяных кристаллических частиц. Основной целью такого исследования является построение адекватной радиационной модели кристаллической облачности с учетом многократного рассеяния. Рассмотрены два алгоритма численного моделирования переноса излучения, основанных на методе Монте-Карло и трассировке лучей. Первый алгоритм можно назвать традиционным. Он хорошо известен и широко используется многими авторами для оценки линейных функционалов от решения уравнения переноса оптического излучения в изотропных средах, в которых индикатрисы рассеяния не зависят от направления движения световых квантов, а являются функциями углов рассеяния. Этот алгоритм адаптирован к задачам переноса излучения в анизотропных кристаллических средах. Применение его для кристаллических сред требует получения и хранения значительного объема начальных данных о первичных оптических характеристиках (коэффициенты ослабления и трехмерные матрицы рассеяния излучения), необходимых для моделирования процессов рассеяния. Этот объем особенно возрастает для неоднородных стохастических рассеивающих сред, в которых форма, размер и ориентация частиц являются случайными функциями от пространственных координат. Ключевая идея второго, альтернативного, алгоритма заключается в том, что в процессе моделирования траекторий фотонов направление рассеяния светового кванта после столкновения с кристаллом моделируется с использованием трассировки лучей при условии, что предварительно случайно выбраны форма, размер и ориентация частицы из некоторого случайного распределения, задающего состав рассеивающей среды. В этом алгоритме нет необходимости предварительных расчетов большого массива данных о первичных оптических характеристиках рассеивающих сред. Алгоритм имеет ограничение на размеры кристаллических частиц: их линейный размер должен значительно превосходить длину волны излучения, так как при моделировании углов рассеяния используются законы геометрической оптики и не учитываются волновые эффекты.
Представлена оптимальная форма записи методов типа Розенброка с точки зрения числа ненулевых параметров и вычислительных затрат на шаге. Получены условия согласованности и устойчивости, теоремы сходимости решения (m, k)-схем для задач индекса два и ниже. Разработан L-устойчивый (5, 4)-метод четвёртого порядка точности, для которого требуются одно вычисление матрицы Якоби и одна LU-декомпозиция на шаге. На базе метода сформулирован алгоритм интегрирования переменного шага, позволяющий решать как явные, так и неявные системы ОДУ. Приведены численные результаты, подтверждающие эффективность алгоритма.
Построен алгоритм переменной структуры на основе явных методов Рунге-Кутты с расширенными областями устойчивости порядка согласованности до трёх и (m, k)-схемы четвёртого порядка точности.